Matriz Inversa
La matriz inversa es un punto de paso obligatorio en álgebra lineal. Ya que debemos de asegurarnos que es una matriz invertible antes de calcularla.
¿Qué es una matriz inversa?
Podemos llamarlo como matriz invertible a una matriz, cuando existe otra matriz que puede ser considerada su inversa. Una matriz es invertible si se puede calcular su inversa, de forma que la matriz por su inversa de lugar a una matriz identidad. Significa que A x A-1 =1.Se dice que una matriz invertible es una matriz regular, no singular, o no denegada. pero existe la posibilidad de que una matriz posea más de una inversa.
Propiedades de la matriz inversa.
Debemos conocer las propiedades de la matriz inversa para entender la mayoría de operaciones que se vaya a realizar.
La inversa de un producto de matrices es igual al producto de la inversa de cada matriz (AxB)-1=A-1 x B-1.
La inversa de la matriz inversa es la matriz natural: (A-1)-1
![]()
![]()
![]()
![]()
Método para calcular la matriz inversa.
Hay diferentes métodos para calcular la inversa de una matriz. Si una matriz es invertible podemos calcular su inversa a partir del método por determinantes, el método de Gauss-Jordan y el método por adjuntos. Sea cual sea el orden para cuantificar la matriz inversa, el resultado debe ser el mismo, ya que una matriz solo tiene un opuesto.
Por ejemplo, si A es dimensión 2x2,
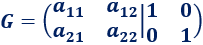




Hola Dina, veo que esta haciendo un buen trabajo.
ResponderEliminarSeria bueno ponerle justificar a los párrafos para que se vea formal.
Pienso que debería de poner algún ejemplo de la matriz inversa.
Pero aun tenemos tiempo para poder verificar y agregar lo que hace falta.
Bendecido día.