ANÁLISIS COMBINATORIO
Es la rama de la matemática que estudia los diversos arreglos o agrupaciones que podemos formar con los elementos de un conjunto dado, conformándolas y calculando su número permitiéndonos resolver problemas de la vida real.
Principios del análisis combinatorio.
El análisis combinatorio se define como una manera práctica y abreviada de contar, las operaciones o las actividades que se presentan son designadas como eventos o sucesos.
Ejemplo.
En la etapa final de fútbol de la Copa Perú
Solución:
- MÉTODO 1: utilizando el diagrama del árbol
Existen 6 maneras diferentes en que estos equipos pueden ubicarse en el primer y segundo lugar, es decir campeón y sub-campeón.
Variaciones sin repetición
Las variaciones sin repetición de "n" elemento tomado de "p" en "p" se define como las distintas agrupaciones formadas con "p" elementos distintos, eligiéndolos de entre los n elementos de que disponemos, considerando una variación distinta a otra tanto si define en algún elemento como si están situados en distintos orden.
El número de variaciones que se pueden construir se puede calcular mediante la fórmula.
Estas variaciones son llamadas lineales, porque los elementos son ordenados en una línea recta de referencia.
Ejemplo:
Se desea elaborar una bandera de dos franjas, se tiene telas de los colores: blanco, azul y rojo. Calcula cuantos tipos de banderas se pueden elaborar.
Solución:
Método 1:
Blanco = b
Azul = a
Rojo = r
Se tiene el conjunto de telas de colores {b, a, r}, entonces los arreglos serían:
ba, br, ab, ar, rb, ra
Entonces, el número de arreglos es 6
Método 2: (principio de multiplicación)
.png)
Permutaciones
Las permutaciones o también llamadas, ordenaciones son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que.
Influye el orden en que se colocan.
Tomamos todos los elementos de que se dispone.
Permutaciones sin repetición
Las permutaciones sin repetición de n elementos se definen como las distintas formas de ordenar todos esos elementos, por lo que la única diferencia entre ellas es el orden de colocacion de sus elementos.
Ejemplo:
Calcula el número de palabras de 3 letras se pueden formar con las letras “a, n, e”
Solución
Para hallar el número de permutaciones circulares que se pueden formar con "n" objetos distintos de un conjunto, hay que considerar fija la posición de un elemento, los n -1 restantes podrán cambiar de lugar de (n-1) Formas diferentes tomando todas las posiciones sobre la circunferencia relativa al primer punto.
El número de permutaciones circulares se calcula con la fórmula.
Ejemplo1:
¿De cuántas formas diferentes puede sentarse al rededor de una mesa circular un padre y sus 5 hijos?
Solución:
Combinaciones
Las combinaciones son aquellas formas de agrupar los elementos de un conjunto teniendo en cuenta que:
- No influye el orden en que se colocan.
- Si permitimos que se repitan los elementos, podemos hacerlo hasta tantas veces como elementos tenga la agrupación.
Combinaciones sin repetición
Son arreglos lineales de los elementos de un conjunto en los que no se toma en cuenta el orden de colocación de cada arreglo.
Dos arreglos son diferentes si contiene un elemento que no contiene el otro.
El número de combinaciones de “n” elementos de un conjunto, todos distintos, tomados de “p” en “p” , con p £ n ,es igual a:
Ejemplo:
Una señora tiene 3 frutas : fresa, uva y papaya. ¿Cuántos sabores diferentes de jugo podrá preparar con estas frutas ?
Método 1
Cuando se escoge una fruta de las tres, los sabores son 3: F, U ,P
Cuando se escoge 2 de las tres frutas, los sabores son 3: FU, FP, UP
Cuando se escoge las 3 frutas los sabores son 1: FUP
Total de sabores diferentes : 3 + 3 + 1 = 7
Método 2
Se puede escoger una fruta de las tres ó 2 frutas de las tres ó las tres frutas de las tres, además en este caso no importa el orden; por lo tanto usamos el principio de adición aplicado a la combinación:
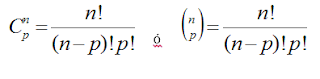
Comentarios
Publicar un comentario