Matriz inversa 3x3
En matemáticas y en álgebra lineal, una matriz cuadrada A de orden n se dice que es invertible, no singular, no pervertido o regular si existe otra matriz cuadrada de orden n, llamada matriz inversa de A y representada como A-1 tal que AA-1= A-1A=I donde I es la matriz similitud de orden n y el producto utilizado es el producto de matrices usual.
Una matriz no invertible se dice que es singular o degenerada. Una matriz es único si y solo si su determinante es cero.
La inversión de matrices es el proceso de encontrar la matriz inversa de una matriz dada.
Ejemplo
Matriz inversa3x3
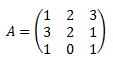
Calcular los elementos de la matriz adjunta de A.
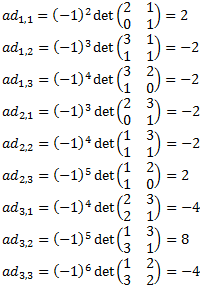
La matriz adjunta de A es.
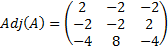
Calcular el determinante de A.
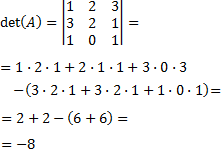
La matriz inversa de A es.
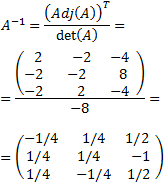


Comentarios
Publicar un comentario