Distribución de Probabilidades.

La distribución de probabilidad de una variable aleatoria es una función que asigna a cada suceso definido sobre la variable la probabilidad de que dicho suceso ocurra. La distribución de probabilidad está definida sobre el conjunto de todos los sucesos y cada uno de los sucesos es el rango de valores de la variable aleatoria.

Distribución de la variable discreta.

Se denomina distribución de variable discreta a aquella cuya función de probabilidad solo toma valores positivos en un conjunto de valores de ${\displaystyle X}$ finito o infinito numerable. A dicha función se le llama función de masa de probabilidad. En este caso la distribución de probabilidad es la suma de la función de masa, por lo que tenemos entonces que:

${\displaystyle F(x)=P(X\leq x)=\sum _{k=-\infty }^{x}f(k)}$

Y, tal como corresponde a la definición de distribución de probabilidad, esta expresión representa la suma de todas las probabilidades desde ${\displaystyle -\infty }$ hasta el valor ${\displaystyle x}$.

Distribución de variable continua.

Se denomina variable continua a aquella que puede tomar cualquiera de los infinitos valores existentes dentro de un intervalo. En el caso de variable continua la distribución de probabilidad es la integral de la función de densidad, por lo que tenemos entonces que:

${\displaystyle F(x)=P(X\leq x)=\int _{-\infty }^{x}f(t)\,dt}$

Ejemplo.

Por ejemplo, para el tiro de un dado (6 caras) la función de distribución de que salga 5 o menos sería la suma de probabilidades de que salga 1, 2, 3, 4 y 5, es decir 1/6+1/6+1/6+1/6+1/6 = 5/6. 

Distribución binomial

Es una distribución discreta muy importante que surge en muchas aplicaciones bioestadísticas. Fue obtenida por Jakob Bernoulli (1654-1705) y publicada en su obra póstuma Ars Conjectandi en 1713. Esta distribución aparece de forma natural al realizar repeticiones independientes de un experimento que tenga respuesta binaria, generalmente clasificada como “éxito” o “fracaso”; este experimento recibe el nombre de experimento de Bernoulli. Ejemplos de respuesta binaria pueden ser el hábito de fumar (sí/no), si un paciente hospitalizado desarrolla o no una infección, o si un artículo de un lote es o no defectuoso. La variable discreta que cuenta el número de éxitos en n pruebas independientes de ese experimento, cada una de ellas con la misma probabilidad de “éxito” igual a p, sigue una distribución binomial de parámetros n y p, que se denota por (Bi(n,p)). Este modelo se aplica a poblaciones finitas de las que se toman elementos al azar con reemplazo, y también a poblaciones conceptualmente infinitas.

Ejemplo.

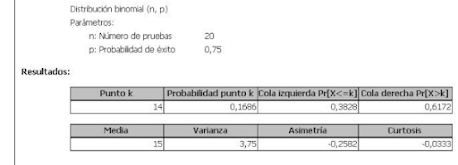
En un examen formado por 20 preguntas, cada una de las cuales se responde declarando “verdadero” o “falso”, el alumno sabe que, históricamente, en el 75% de los casos la respuesta correcta es “verdadero” y decide responder al examen tirando dos monedas: pone “falso” si ambas monedas muestran una cara y “verdadero” si al menos hay una cruz. Se desea saber cual es la probabilidad de que tenga más de 14 aciertos. Hay que proporcionarle a Epidat 4 los parámetros de la distribución binomial y el punto k a partir del cual se calculará la probabilidad. En este caso n = 20, p = 0,75 y el punto k = 14.

La probabilidad de que el alumno tenga más de 14 aciertos es del 62%. El programa, además de calcular probabilidades, proporciona los valores característicos de la distribución (media, varianza, asimetría y curtosis) como información complementaria. Esta información depende solo de los parámetros de la distribución, no se ve influida por la opción elegida a la hora de realizar el cálculo (probabilidades o puntos) ni por el punto o probabilidad sobre el que se realiza dicho cálculo. En este ejemplo, la media indica que 15 es el número medio de aciertos mediante la técnica de tirar dos monedas.

                          DISTRIBUCIÓN DE POISSON

En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad de que ocurra un determinado número de eventos durante cierto período de tiempo.

Formalmente : dada una variable aleatoria X con campo de variación

X Î {0,1,2,..., ¥ }, es decir X Î N cuya función de cuantía sea:

 siendo l un parámetro positivo

diremos que X sigue una distribución de Poisson de parámetro l , X ~ P(l ).

Si en estas circunstancias la variable aleatoria X = nº de hechos que se producen en un intervalo unitario sigue una distribución de Poisson , que cómo veremos tendrá por parámetro l el número medio de hechos que pueden producirse en el intervalo unitario.

distribución de Poisson:

f (t) = E(e^tx) = S e^tx P(x) = = =

Derivando sucesivamente podremos obtener los distintos momentos ordinarios y, a partir de ellos media, varianza y otros indicadores:

f ' (t) = l e^t e^{l(et - 1)} ¾ ¾ ¾ ® f ' (t =0) = a₁= m = l

f '' (t) = l e^t e^{l(et - 1)} +( l e^t )² e^{l(et - 1)} ¾ ¾ ¾ ®

¾ ¾ ¾ ® f ' (t =0) = a₂= l + l²

de forma que la varianza será: s² = a₂- m² = l + l² - l² = l

 

La moda de una distribución de Poisson puede determinarse como el valor de la variable (el número natural) que verifica que:

l - 1 £ Mo £ l

Ejemplo

La veterinaria de Jorge recibe un promedio de μ = 4 pacientes por día. Sabiendo que el número de pacientes que llegan en un día sigue una distribución de Poisson.

a) la probabilidad de que lleguen 3 pacientes en un día.

Primero definimos nuestra variable aleatoria:

X = número de pacientes que llegan en un día.

Además, nos indican que esta variable aleatoria X sigue una distribución de Poisson, entonces podemos aplicar la fórmula:

f(x)=P(X=x)=e−μ⋅μxx!$$f(x)=P(X=x)=\frac{e^{-\mu }\cdot {\mu }^x}{x!}$$

Calculamos la probabilidad de que lleguen 3 pacientes en un día, es decir, f(3). Además, el enunciado nos indica que llegan en promedio 4 pacientes por día, es decir, μ = 4.

f(3)=P(X=3)=e−4⋅433! f(3)=P(X=3)=0,01832⋅643⋅2⋅1 f(3)=P(X=3)=0,1954$$\begin{gathered} f(3)=P(X=3)=\frac{e^{-4}\cdot 4^3}{3!} \\ f\left(3\right)=P(X=3)=\frac{0,01832\cdot 64}{3\cdot 2\cdot 1} \\ f(3)=P(X=3)=0,1954 \end{gathered}$$

La probabilidad de que lleguen 3 pacientes en un día es de 0,1954 o 19,54 %.

b) la probabilidad de que lleguen 5 pacientes en un día.

Calculamos la probabilidad de que lleguen 5 pacientes en un día, es decir, f(5). Además, el enunciado nos indica que el enunciado que llegan en promedio 4 pacientes por día, es decir, μ = 4.

f(x)=P(X=x)=e−μ⋅μxx! f(5)=P(X=5)=e−4⋅455! f(5)=P(X=5)=0,01832⋅10245⋅4⋅3⋅2⋅1 f(5)=P(X=5)=0,1563$$\begin{gathered} f(x)=P(X=x)=\frac{e^{-\mu }\cdot {\mu }^x}{x!} \\ f(5)=P(X=5)=\frac{e^{-4}\cdot 4^5}{5!} \\ f\left(5\right)=P(X=5)=\frac{0,01832\cdot 1024}{5\cdot 4\cdot 3\cdot 2\cdot 1} \\ f(5)=P(X=5)=0,1563 \end{gathered}$$

La probabilidad de que lleguen 5 pacientes en un día es de 0,1563 o 15,63 %.